Die Magie der Backpropagation

Dieser Artikel ist sozusagen die Fortsetzung des Artikels Neuronale Netze einfach erklärt, in welchem ich mit der Frage aufgehört habe, wie Backpropagation eigentlich genau funktioniert. Diese Frage möchte ich nun in diesem Artikel behandeln, genau genommen zwei Aspekte, die ich bei der Backpropation hervorheben möchte.

Falls ihr den vorherigen Artikel noch nicht gelesen habt, aber bereits wisst wie ein Neuronales Netz aufgebaut ist, dann sollte das soweit reichen. Auch setze ich Basiswissen in Calculus (zu Deutsch Analysis), oder im Grunde genommen nur Ableitungen, vorraus.

Neuronales Netz

Als Beispiel Neuronales Netz betrachte ich wieder das selbe Neuronale Netz wie auch schon in Neuronale Netze einfach erklärt.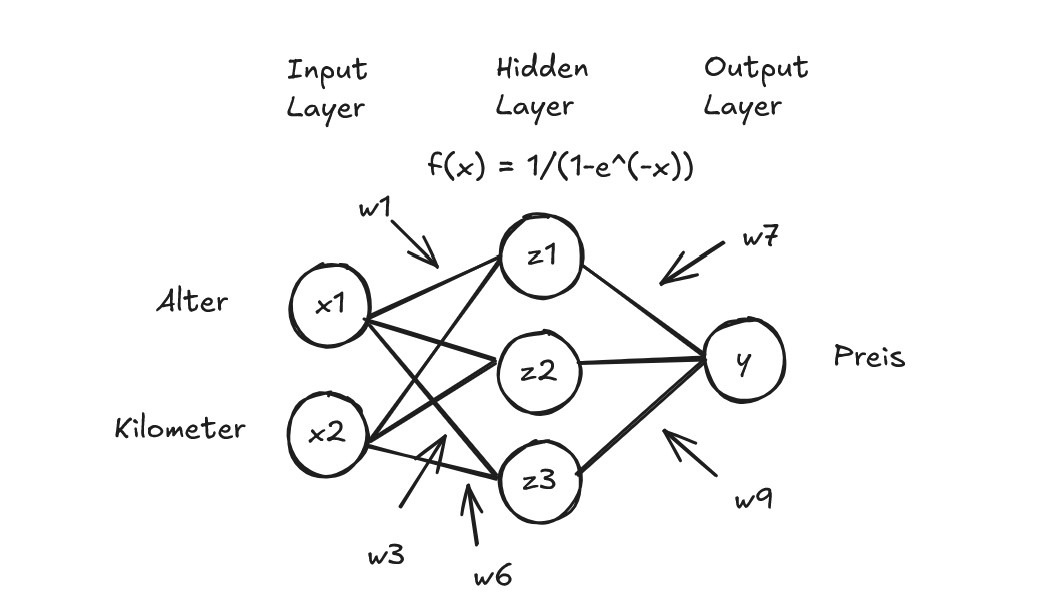Wobei ich noch Variablenbezeichner hinzugefügt habe. Die Variablen in den Neuronen beziehen sich auf die Werte der Neuronen. Die Variablen für die Weights habe ich so durchnummeriert, dass die Weights der Neuronen von oben nach unten nummeriert sind.

Eine interessante Perspektive ist, dass man das Neuronale Netz auch als Funktion sehen kann. Es hat 2 Inputs (Funktionsparameter), nämlich Alter = x1, Kilometer = x2 und es berechnet 1 Output, den vorhergesagten Preis = y.

$$f(x_1, x_2) = y$$

Aber dabei sind im Grunde nicht nur die beiden Inputs des Neuronalen Netzes Funktionsparameter, sondern auch die Weights. Wenn die Weights verändert werden, dann verändert sich auch y. Somit kann man das Neuronale Netz auch als diese Funktion f formalisieren.

$$f(x_1, x_2, w_1, w_2, \dots, w_8, w_9) = y$$

Der Wert y wird aus den Werten z1, z2, z3 und den dazugehörigen Weights berechnet, somit kann man diese auch einsetzen.

$$f(x_1, x_2, w_1, w_2, \dots, w_8, w_9) = z_1w_7 + z_2w_8 + z_3w_9 = y$$

Wenn man dasselbe für z1, z2, z3 macht, erhält man eine ziemlich große Formel, welche aber rein aus den Funktionsparameter und Operationen zwischen diesen besteht.

$$f(x_1, x_2, w_1, w_2, \dots, w_8, w_9) = \\ g(x_1w_1 + x_2w_4)w_7 + g(x_1w_2 + x_2w_5)w_8 + g(x_1w_3 + x_2w_6)w_9 = y$$

Wobei g hier die Aktivierungsfunktion ist, also in unserem Beispiel die Sigmoid Funktion. Man sieht, das ist durchaus nicht allzu simpel und die Ansicht als Netz von Neuronen ist übersichtlicher. Aber es macht trotzdem Sinn im Kopf zu behalten, dass das Neuronale Netz im Grunde auch nur eine Funktion ist und wir sie so niederschreiben können.

Daten

Ein Neuronales Netz soll aus Daten lernen, dieser Prozess wird auch Training genannt und ist im Grunde iteratives anwenden von Backpropagation. Daher sind Daten ein sehr wichtiger Aspekt beim Erstellen eines Neuronalen Netzes. Im Folgendem hab ich mir mal für unser Beispiel 3 Datenpunkte ausgedacht.

Loss Function

Bevor wir uns der Backpropagation widmen, benötigen wir noch eine weitere wichtige Konstruktion. Wir haben den wahren Wert für den Preis eines Autos, nennen wir ihn mal yw (y „wahr“) und auch den berechneten Preis aus dem Neuronalen Netz, y. Wenn wir diese subtrahieren und dann quadrieren, erhalten wir die Loss Function. Als Formel:

$$L = (f(x_1, x_2, w_1, w_2, \dots, w_8, w_9) – yw)^2 = (y \; – \; yw)^2$$

Die Loss Function ist implizit eine Funktion der NN-Parameter als auch der Eingangswerte und zusätzlich eben noch des wahren Preises. Was aber ist das Ziel dieser Konstruktion? Nun die Loss Function hat eine interessante Eigenschaft, nämlich wenn unser Neuronales Netz den Preis richtig vorhersagt, dann ist der Wert der Loss Function 0. Das machen wir uns während der Backpropagation zu Nutze, indem wir uns zu einem Minimum bewegen, aber mehr dazu später.

Ist gibt auch noch andere Loss Function, zum Beispiel könnte man auch den absoluten Wert der Differenz von y und yw nehmen. Beide diese Loss Functions haben, aber die wichtige Eigenschaft immer größer 0 zu sein, das wird benötigt bei der Cost Function.

Cost Function

Der arithmetische Durchschnitt über alle Loss Functions ist die Cost Function. Manchmal wird Cost und Loss Function auch synonym verwendet.

Die Cost Function ist, weil wir nur drei Datenpunkte haben, für unser Beispiel dann (L_1 ist die Loss Function des ersten Datenpunkts):

$$C = \frac{L_1 + L_2 + L_3}{3}$$

Weil die jeweiligen Loss Function immer größer als 0 sind, wissen wir das wenn die Cost Function 0 ist, müssen auch alle Loss Functions 0 sein, was dann bedeutet, dass unser Neuronales Netz alles exakt vorhersagt. Also müssen wir nur unsere NN-Parameter so anpassen, dass unsere Cost Function 0 wird. Und das passiert mit der Backpropagation.

Backpropagation

Die grobe Idee der Backpropagation ist mittels der Ableitung, genau genommen der partiellen Ableitung, der Cost Function, die Parameter des Neuronalen Netzes sinnvoll anzupassen. Ich möchte, um den Unterschied der Backpropagation zu „normaler“ Ableitung, wie man sie aus dem Schulunterricht vielleicht kennt, auf zwei Besonderheiten eingehen. Die erste ist der Gradient.

Gradient

Da wir die Ableitung nicht analytisch exakt berechnen können, berechnen wir stattdessen eine sozusagen approximative Ableitung, nämlich den Gradienten und das tun wir mithilfe von Daten. Was aber mein ich mit analytisch nicht berechnen können? Nehmen wir zum Beispiel die simple Funktion

$$f(x) = x^2$$

Ich kann einen beliebigen reellen Wert einsetzen und erhalte dafür den dazugehörigen Funktionswert. Das bedeutet es, eine analytisch Form einer Funktion zu haben. Basierend darauf kann man auch sehr leicht die Ableitung von x^2 berechnen, wenn man sich noch an die Ableitungsregeln erinnert, die ich hier mal der Vollständigkeit halber aufliste:

1. Power Rule:
\[
\frac{d}{dx}(x^n) = n x^{n-1}
\]

2. Sum/Difference Rule:
\[
\frac{d}{dx}(f(x) \pm g(x)) = f'(x) \pm g'(x)
\]

3. Product Rule:
\[
\frac{d}{dx}(f(x) \cdot g(x)) = f'(x) g(x) + f(x) g'(x)
\]

4. Quotient Rule:
\[
\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x) g(x) – f(x) g'(x)}{g(x)^2}
\]

5. Chain Rule:
\[
\frac{d}{dx} f(g(x)) = f'(g(x)) \cdot g'(x) = \frac{df}{dg} \cdot \frac{dg}{dx}
\]

Die Ableitung von x^2 kann man nun sehr simpel mit der Power Rule bestimmen und ist:

$$f(x) = 2x$$

Wenn wir aber nun die Loss Function betrachten:

$$L = (f(x_1, x_2, w_1, w_2, \dots, w_8, w_9) \; – \; y_w)^2 = (y \; – \; y_w)^2$$

Dann sehen wir, dass wir das Neuronale Netz (f) analytisch berechnen können, aber das yw nicht (wenn wir das könnten bräuchten wir ja auch überhaupt kein Neuronales Netz). Also müssen wir den Gradienten berechnen und das tun wir mithilfe von Funktionswerten, die wir bereits kennen. Mit Funktionswerten mein ich im Grunde die Eingangswerte und Ausgangswerte der Funktion, die wir modellieren wollen (also wie der Kilometer / Alter den Preis beinflussen). Durch unsere 3 Datenpunkte haben wir auch 3 Sets solcher Funktionswerte.

Berechnung eines Gradienten

Wie bereits erwähnt müssen wir die Ableitung der Loss Function nach einem der Parameter berechnen, oder um genauer zu sein die partielle Ableitung, aber die unterscheidet sich im Grunde nicht (wirklich) von der normalen Ableitung.

Betrachten wir also die Loss Function mit dem heruntergebrochenen Neuronalen Netz:

$$L = (y \; – \; y_w)^2 = (f(x_1, x_2, w_1, w_2, \dots, w_8, w_9) \; – \; y_w)^2 = \\ (g(x_1w_1 + x_2w_4)w_7 + g(x_1w_2 + x_2w_5)w_8 + g(x_1w_3 + x_2w_6)w_9 \; – \; y_w)^2$$

Und hier nehmen wir nun die Ableitung nach w1 was dann, nachdem man die Kettenregel (Chain Rule) und andere einfache Ableitungsregeln anwendet, wie folgt aussieht:

$$\frac{dL}{dw_1} = 2 \cdot (g(x_1w_1 + x_2w_4)w_7 + g(x_1w_2 + x_2w_5)w_8 + g(x_1w_3 + x_2w_6)w_9 \; – \; y_w) \cdot g'(x_1w_1 + x_2w_4)w_7 \cdot x_1 \\ = 2 \cdot (y \; – \; y_w) \cdot g'(x_1w_1 + x_2w_4)w_7 \cdot x1$$

wobei g die Sigmoid Funktion ist. Was die genaue Ableitung der Sigmoid Funktion ist, ist auch nicht unbedingt wichtig, solange man sie berechnen kann (was ich hier für euch machen werde). Wir sehen hier aber ein paar Variablen, zum einen das Set von Funktionwerten x1, x2, yw, wo wir einen Datenpunkt einsetzen können, zum Beispiel den ersten Datenpunkt also 1, 2000, 11000.

Was aber auch auffällt, das noch gar nicht klar ist welche Startwerte die Weights haben sollten. Nun da wir nicht wissen, welche Werte für die Parameter am besten sind beginnt man mit zufällig ausgewählten Werten. Ich habe mal ein paar Werte zufällig generiert.

$$w_1 = 0.003603, w_2 = 0.002676, w_3 = -0.004249, w_4 = 0.005574, \\ w_5 = -0.00215, w_6 = 0.006055, w_7 = -0.6448, w_8 = -0.0231, w_9 = -0.3891$$

Jetzt kann man all diese Werte einsetzen um den Gradienten (basierend auf dem 1. Datenpunkt) zu berechnen:

$$\frac{dL}{dw_1} = 2 \cdot (y \; – \; y_w) \cdot g'(x_1w_1 + x_2w_4)w_7 \cdot x1 = \\ 2 \cdot (-1.034 \; – \; 11000) \cdot g'(1 \cdot 0.003603 + 2000 \cdot 0.005574) \cdot -0.6448 \cdot 1 \\ = 0.641$$

Learning Rate

Dieser Wert also Gradient gibt an wie wir den Parameter w1 anpassen (also den Gradienten zu dem Parameter addieren) sollen um den Loss zu erhöhen, da wir aber den Loss auf 0 reduzieren wollen, müssen wir stattdessen das Negative davon nehmen. Aber nicht nur diese Anpassung sollten wir vornehmen, sondern auch noch den Gradienten mit der sogenannten Learning Rate multiplizieren. Meist wird dafür eine Learning Rate von 0.01 gewählt.

Der Grund für das anpassen des Gradienten, ist das der Gradient sonst eine zu große Veränderung verursacht (was oftmals negativ ist, aber nicht unbedingt immer). Zum Beispiel haben wir bei der Berechnung des Gradienten die anderen Weights gleich gelassen, aber wir werden ja auch die anderen Weights anpassen und diese Anpassung ist nicht mit eingerechnet im Gradient des einzelnen Weights. Somit muss mit moderat sein mit der Veränderung durch den Gradienten, was die Learning Rate sicherstellt.

Aktualisierung des Weights

Das angepasste Weight mit einer Learning Rate von 0.01 ist dann:

$$w_1 := w_1 \; – \; \frac{dL}{dw_1} \cdot lr = w_1 \; – \; 0.641 \cdot 0.01 = 0.003603 \; – \; 0.00641 = -0.002807$$

Man sieht hier auch das der Gradient ein Wert ist und nicht eine analytische Funktion, was man normalerweise beim Berechnen einer Ableitung erwarten würde. Dies liegt daran, dass wir das Set an Funktionswerten (den Datenpunkt) eingesetzt haben. Nun berechnet man natürlich den Gradient nicht nur von w1 sondern von allen 9 Parametern und aktualisiert die Weights dann genauso, also mit der folgenden Formel:

$$w_x := w_x \; – \; \frac{dL}{w_x} \cdot lr$$

wobei lr die Learning Rate ist. Das war dann die Anpassung mit dem 1. Datenpunkt, als nächstes geschieht dasselbe mit dem 2. Datenpunkt, also sprich für alle Parameter den Gradient berechnen und dann den Parameter mit dem Gradienten aktualisieren. Selbiges für den 3. Datenpunkt und dann beginnt es wieder mit dem 1. Datenpunkt. Wenn einmal alle Datenpunkte verwendet wurden, nennt man das eine Epoch. Der Loss sollte sich, wenn das Modell gut konfiguriert ist, ungefähr so verhalten:

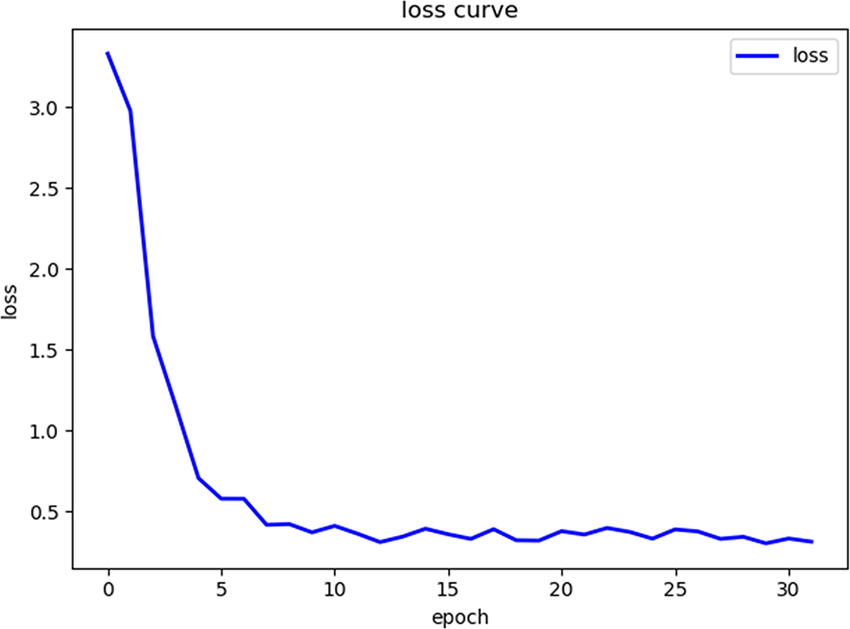
Das Endziel ist es den Loss zu verringern, was hier zu sehen ist (das ist nicht unser Beispielmodell sondern nur ein Beispiel wie es aussehen kann / sollte).

Chain Rule

Die Kettenregel für Ableitungen hat bei Neuronalen Netzen nochmal eine extra wichtige Relevanz, weil man sich damit Arbeit sparen kann und die Gradienten effizienter berechnen kann. Das ist der zweite wichtige Aspekt der Backpropagation (wobei mehr wichtig für die Effizienz). Zum Beispiel haben bei der Beispiel Gradientenberechnung einfach direkt abgeleitet, aber die Kettenregel zeigt dass wir auch stattdessen erst nach y hätten ableiten können und dann y noch nach w1 ableiten. Mathematisch ausgedrückt:

$$\frac{dL}{dw_1} = \frac{dL}{dy} \cdot \frac{dy}{dw_1}$$

Intuitiv ist die Kettenregel der Ausdruck, das wenn es noch eine Zwischenvariable gibt, man einfach über diese die Ableitung / den Gradienten berechnen kann. Als würde man den Bruch erweitern, auch wenn das mathmatisch formell nicht ganz so korrekt ist. Nun können wir einmal den Gradienten von L nach y berechnen:

$$\frac{dL}{dy} = \frac{d}{dy} (y \; – \; y_w)^2 = 2 \cdot (y \; – \; y_w) \cdot 1 \\ = 2 \cdot (y \; – \; y_w) = 2 \cdot (-1.034 \; – \; 11000) = -22002.068$$

Das ist wenn man zurückschaut, auch genau der linke Teil beim berechnen des Gradienten von w1 und der rechte ist dann eben der Gradient von y nach w1. Das wirklich interessante ist aber, dass wir all die Gradienten der anderen Parameter genauso berechnen können, also:

$$\frac{dL}{dw_x} = \frac{dL}{dy} \cdot \frac{dy}{dw_x} = -22002.068 \cdot \frac{dy}{dw_x}$$

Somit sparen wir uns Berechnungen und sind deutlich effizienter. Dies ist besonders wichtig, sobald das Neuronale Netz größer wird (wir haben hier nur ein sehr kleines Beispiel mit 9 Parametern andere Neuronale Netze haben Parameter in Millionengröße oder noch mehr).

Backpropagation – Zusammenfassung

Jetzt habe ich über die theoretischen Hintergründe der Backpropagation, aber wie genau setzt man es in der Praxis um? Dafür gibt es große optimierte Packages / Libraries, ein Beispiel in der Python Welt ist Pytorch, mit dem man Neuronale Netze definieren kann und die Backpropagation automatisch durchgeführt wird. Das Prinzip ist aber dasselbe wie ich es hier beschrieben habe.

Backpropagation / Trainings Algorithmus

Ich möchte nochmal grob den Algorithmus beschreiben der beim Training (im Grunde das Durchführen der Backpropagation mit Aktualisierung) durchlaufen wird.

1. Berechnung des Outputs des Neuronalen Netzes mit Datenpunkt als Eingangswert (Forward)
2. Gradientenberechnung für alle Parameter (Backpropagation)
3. Aktualisierung der Parameter unter Einbezug der Learning Rate (Update)
4. Nächster Datenpunkt

Falls ihr noch mehr Details und auch das implementieren (in Code) eines Neuronalen Netzes, in zum Beispiel Pytorch, lernen wollt, kann ich auch sehr die Videoreihe von Andrej Karpathy „Neural Networks: Zero to Hero“ (ist auf Englisch) empfehlen, hier der Link zu der Videoreihe.

Matrizen und Linear Transformationen

Was ich noch erwähnen wollte nach diesen beiden Artikeln zu Neuronalen Netzen, ist das wenn man sich ein wenig umschaut, man im Zusammenhang mit Neuronalen Netzen auch immer Matrizen sehen wird, dass hat auch einen guten Grund. Betrachte man zum Beispiel einen Layer mit n Neuronen und den darauffolgenden Layer mit m Neuronen, dann gibt es für jedes Neuron eine Verbindung / ein Weight sprich m * n weights. Die Weights kann man nun genauso in eine mxn Matrix anordnen, dass die Matrixmultiplizierung genau das macht, was ich beschrieben habe, also sprich die Weights mit den Werten der n Neuronen so zu multiplizieren, das man die Werte der m Neuronen des nächsten Layers erhält.

Durch die Matrixdarstellung ist es schöner verpackt und kann auch effizienter berechnet werden. Das Prinzip der Backpropagation funktioniert hier auch, wobei man aber Matrix Calculus verwendet und eine Gradient-Matrix für die jeweilige Weight-Matrix berechnet. Ich habe in den beiden Artikeln das Ganze weggelassen, weils es für die Theorie und das Prinzip von Neuronalen Netzen, nicht direkt erheblich ist, wollte es aber dennoch hier am Ende einmal erwähnt haben.

Abschließend kann man nun aber sagen:

Danke fürs Lesen und alles Gute in eurer Data Science Reise.