Neuronale Netze einfach erklärt

Neuronale Netze sind heutzutage das Aushängeschild des maschinellem Lernens und nicht ohne Grund, wie spätestens ChatGPT der Welt gezeigt hat. Aber wie funktionieren Neuronale Netze? Das möchte ich in diesem Artikel beleuchten, genauer gesagt will ich Neuronale Netze anhand vom Standard Modell als Netz von Neuronen (daher der Name) erklären.

Ein paar Worte zur Terminologie: Sehr viele Begriffe im Bereich Data Science sind englischer Natur, falls sinnvoll werde ich diese übersetzen, aber ansonsten verwende ich den englischen Standardbegriff.

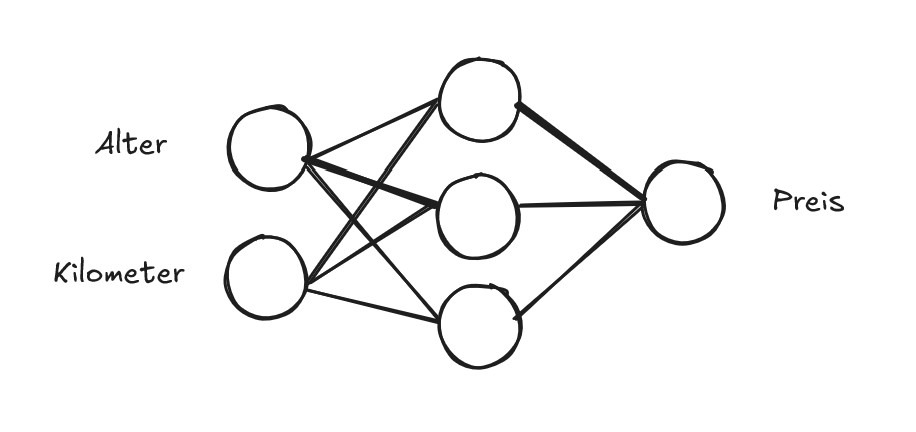
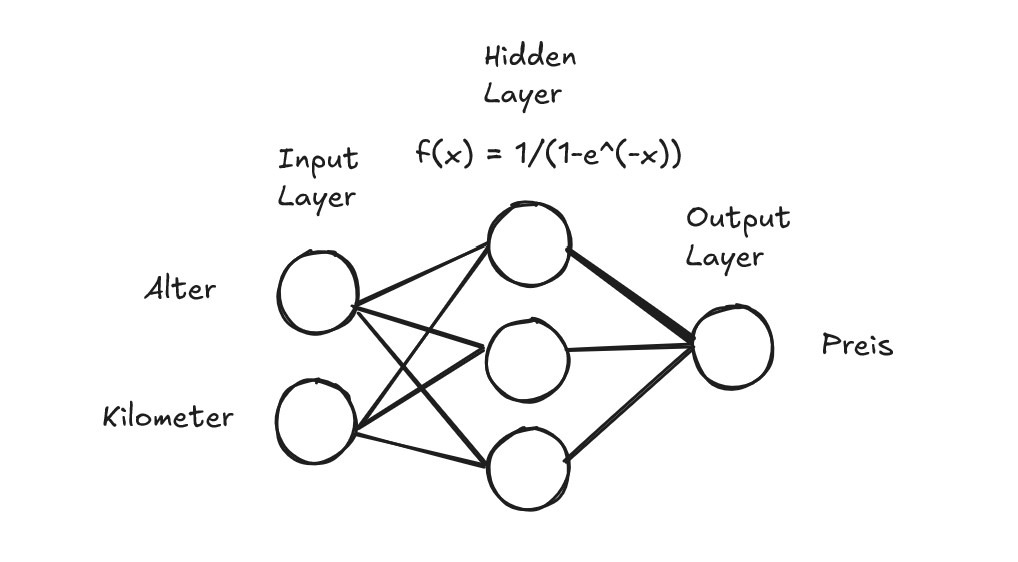
Fangen wir gleich an und wie ginge das besser als mit einem kleinen Beispiel NN (Neuronales Netz).Die Kreise sind die Neuronen und jede Neurone enthält einen Wert. Die beiden Neuronen links sind die Eingangsneuronen, welche die Eingangswerte speichern. In diesem Beispiel wollen wir anhand der beiden Werten, also Alter eines Auto und Kilometer, die das Auto gefahren ist, den Preis des Autos vorhersagen. Ein NN nimmt bestimmte Eingangswerte und berechnet basierend auf diesen Ausgangswerte (ein oder auch mehrere). Wie genau aber berechnet das NN diese Ausgangswerte? Nun bevor wir uns dieser Frage stellen, will ich ein wenig Terminologie einführen.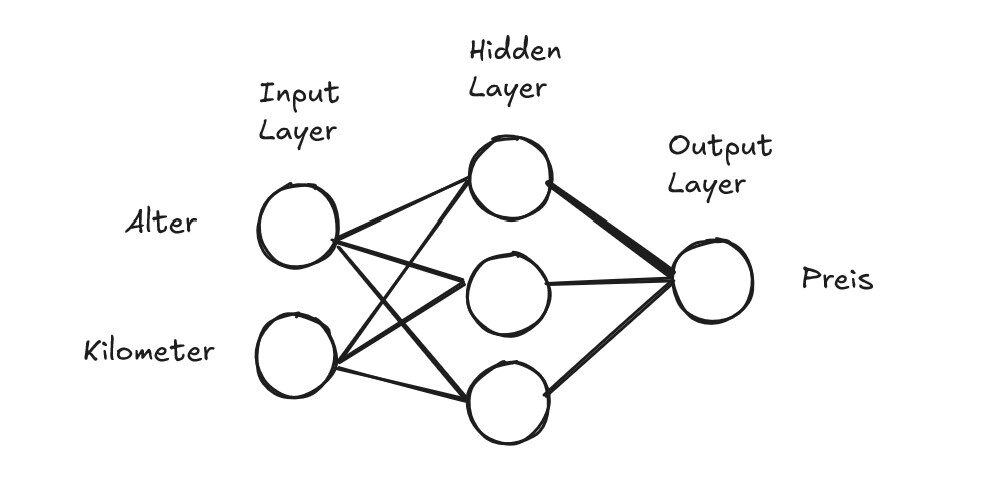

Ein (Standard) Neuronales Netz hat drei Typen von Layern (Schichten). Links ist der Input Layer, mit den Neuronen, welche die Eingangswerte beinhalten, ganz am Ende ist der Output Layer mit den Neuronen, die dann die berechneten Ausgangswerte ausgeben. Und dazwischen befinden sich dann die Hidden Layers, wo sozusagen die Berechnungen durchgeführt werden.

Ein Neuronales Netz kann auch mehrere Hidden Layers und auch beliebig viele Neuronen in eben diesen haben. Um es überschaubar zu halten, habe ich erstmal nur einen Hidden Layer mit 3 Neuronen gewählt. Was ebenfalls wichtig ist, die Neuronen eines Layers sind immer fully connected mit den Neuronen des nächsten Layers. Das bedeutet jedes Neuron von z. B. dem Input Layer hat eine Verbindung zu jedem Neuron des Hidden Layers, wie im Beispiel auch zu sehen ist.

Ein Netz aus Neuronen

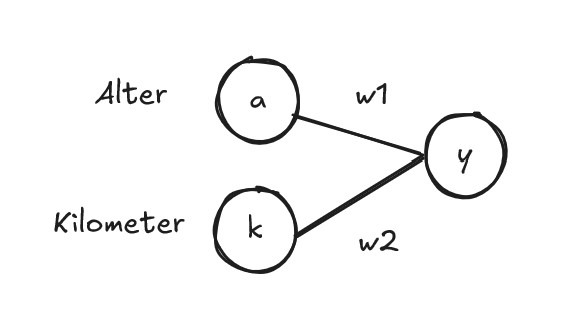
Als nächstes betrachten wir ein Neuron aus dem Hidden Layer isoliert, um zu erklären, was diese Verbindungen genau bedeuten.Diese Verbindungen werden allgemeinhin als weights oder auch Parameter bezeichnet und sind reelle Zahlen. Mithilfe dieser Verbindungen (weights) lässt sich der Wert des Neurons y berechnen, aber wie genau findet das statt? Nun der Wert des eingehenden Neurons wird mit dessen weight multipliziert und die Ergebnisse werden addiert.

$$y = a \cdot w_1 + k \cdot w_2$$

Weil hier nur (mit Skalaren) multipliziert und addiert wird, nennt man diese Layer auch Linear Layer.

Aktivierungsfunktionen in neuronalen Netzen

Ich war nicht ganz ehrlich, denn es gibt noch einen weiteren wichtigen Aspekt um den Wert des Neurons y zu berechnen. Die sogenannte Aktivierungsfunktion ist eine nicht-lineare Funktion, welche auf die Linear Kombination angewandt wird, um das Neuron y zu berechnen (diesmal wirklich):

$$y = f(a \cdot w_1 + k \cdot w_2)$$

wobei f die Aktivierungsfunktion ist. Dieser zusätzliche Schritt ist deshalb so wichtig, weil ein NN sonst nur lineare Prozesse und Zusammenhänge modellieren könnte. Im Grunde keines der Probleme, welche man mit NN lösen will, ist aber linear. In unserem Beispiel würde sich der Preis des Autos auch nicht linear verringern, wenn die gefahrenen Kilometer ansteigen. Somit könnten wir ohne die Aktivierungsfunktion unser Beispiel nicht erfolgreich modellieren. Welche nicht-lineare Funktion wählt man aber als Aktivierungsfunktion? Eine Option ist z. B. die Sigmoid Funktion:

$$f(x) = \frac{1}{1 – e^{-x}}$$

Das sieht erstmal komplex aus, aber der Graph der Sigmoid Funktion ist deutlich simpler.

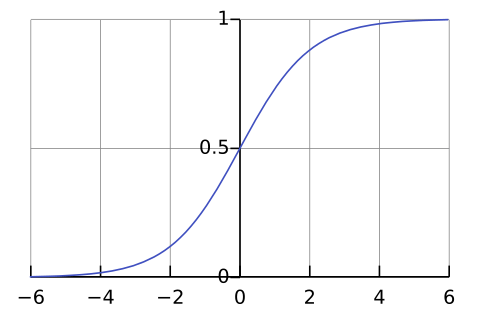
Man sieht das sehr positive Werte zu 1 gemappt werden und sehr negative Werte zu 0. Das kann man als das Pendant zum Aktivieren (daher der Name Aktivierungsfunktion) eines biologischem Neurons interpretieren, also 1 heißt das Neuron feuert und 0 es feuert nicht. Es gibt aber auch andere Aktivierungsfunktionen, die nicht diese charakteristik haben, also ist es keine allgemeine Analogie. Andere Aktivierungsfunktionen sind z. B. ReLu, Tanh und GeLu .

Die Aktvierungsfunktion wird nur bei Neuronen in Hidden Layers angewandt, nicht im Input / Output Layer. In einem Hidden Layer gibt es für alle Neuronen, die selbe Aktivierungsfunktion. In unserem Beispiel könnten wir das wie folgt modellieren:

Zusammenfassung – neuronale Netze

Falls ich dir 9 weights für das Beispiel NN geben würde, könntest du nun also das Beispiel NN durchrechnen. Sprich für ein gegebenes Alter und eine gegebene Kilometeranzahl einen Preis für das Auto berechnen. Das wirft aber die Frage auf wie genau man auf Parameter kommt, mit denen das NN möglichst akkurat den Preis vorhersagt. Im Grunde könnte ich ja irgendwelche 9 Zahlen als weights nehmen, aber das würde nicht garantieren, dass ich am Ende einen sinnvollen Preis berechnen kann (wohl eher das Gegenteil).

Die Lösung dafür ist Backpropagation, was im Grunde die wahre Magie der Neuronalen Netze ausmacht. Um zu erklären wie Backpropagation funktioniert, habe ich diesen Artikel „Die Magie der Backpropagation“ geschrieben, welcher im Grunde eine Fortsetzung dieses Artikels darstellt.

Danke fürs Lesen und alles Gute in eurer Data Science Reise.